Trong bài viết dưới đây, cửa hàng chúng tôi sẽ nói lại những kiến thức về hệ thức lượng trong tam giác vuông, cân, thường giúp chúng ta củng rứa lại kỹ năng vận dụng giải bài tập tiện lợi nhé
Các hệ thức lượng trong tam giác
1. Định lý Cosin
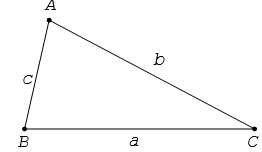
Trong một tam giác bất kì, bình phương một cạnh bởi tổng những bình phương của hai cạnh sót lại trừ đi hai lần tích của nhị cạnh đó nhân cùng với cosin của góc xen thân chúng.
Bạn đang xem: Các định lý trong tam giác vuông
a2 = b2 + c2 – 2bc.cosA;b2 = c2 + a2 – 2ca.cosB;c2 = a2 + b2 – 2ab.cosC.Hệ quả:
Cos A = (b2 + c2 – a2)/2bcCos B = (a2 + c2 – b2)/2acCos C = (a2 + b2 – c2)/2ab2. Định lý Sin
Trong tam giác ABC bất kỳ, tỉ số giữa một cạnh cùng sin của góc đối diện với cạnh đó bằng 2 lần bán kính của mặt đường tròn nước ngoài tiếp tam giác. Ta có:
a /sinA = b/sinB = c/sinC = 2R
Với R là bán kính đường tròn nước ngoài tiếp tam giác
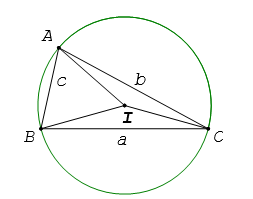
Ngoài ra, các bạn nên đọc thêm công thức lượng giác chi tiết tại đây.
3. Độ dài con đường trung đường của tam giác
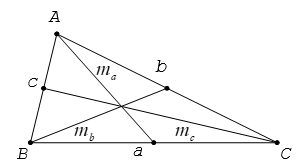
Cho tam giác ABC bao gồm độ lâu năm cạnh BC = a, CA = b, AB = c. điện thoại tư vấn ma, mb, mc thứu tự là độ dài những đường trung tuyến đường vẽ tự đỉnh A, B, C của tam giác.Ta có
ma2 = <2(b2 + c2) – a2>/4mb2 = <2(a2 + c2) – b2>/4mc2 = <2(a2 + b2) – c2>/44. Công thức tính diện tích tam giác
Ta kí hiệu ha, hb với hc là các đường cao của tam giác ABClần lượt vẽ từ những đỉnh A, B, C với S là diện tích tam giác đó.
Diện tích S của tam giác ABC được tính theo một trong số công thức sau:
S = ½absinC = ½bcsinA = ½casinBS = abc/4RS = prS = √p(p – a)(p – b)(p – c) (công thức hê – rông)Hệ thức lượng vào tam giác vuông
1. Những hệ thức về cạnh và đường cao vào tam giác vuông
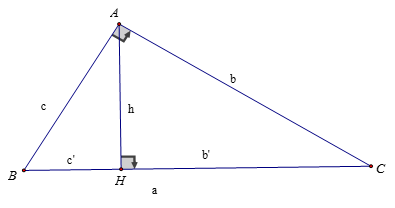
Cho ΔABC, góc A bởi 900, AH ⊥ BC, AB = c, AC = b, BC = a, AH = h thì:
BH = c’ được hotline là hình chiếu của AB xuống BCCH = b’ được hotline là hình chiếu của AC xuống BCKhi đó, ta có:
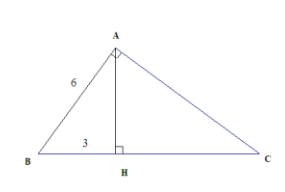
c2 = a.c’ (AB2 = BH.BC) b2 = a.b’ (AC2 = CH.BC)h2 = b’.c’ (AH2 = CH.BH)b.c = a.h (AB.AC = AH.BC )1/h2 = 1/b2 + 1/c2 (1/AH2 = 1/AB2 + 1/AC2)b2 + c2 = a2 (AB2 + AC2 = BC2)(Định lý Pytago)2. Tỉ số lượng giác của góc nhọn
a. Định nghĩa
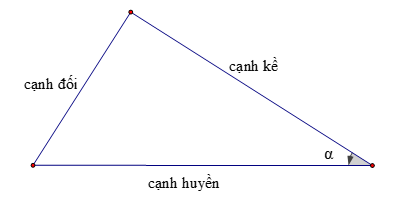
b. Định lí
Nếu hai góc phụ nhau thì sin góc này bởi cosin góc kia, tang góc này bởi cotang góc kia.
c. Một vài hệ thức cơ bản
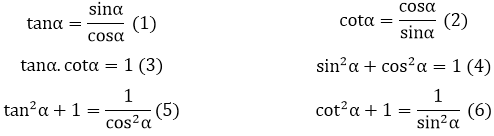
d. So sánh các tỉ số lượng giác
Cho góc nhọn α, ta có:
a) cho α,β là nhị góc nhọn. Giả dụ α sinα cosα > cosβ; cotα > cotβ
b) sinα 2. Hệ thức về góc cùng cạnh trong tam giác vuông
a. Các hệ thức
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
Cạnh huyền nhân với sin góc đối hoặc nhân cùng với cos góc kềCạnh góc vuông tê nhân với rã góc đối hoặc cot góc kề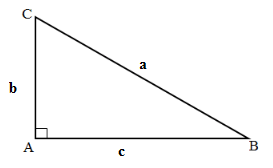
3. Giải tam giác và vận dụng vào vấn đề đo đạc
Giải tam giác : Giải tam giác là tìm một số yếu tố của tam giác khi đã biết các yếu tố không giống của tam giác đó.
Muốn giải tam giác ta đề nghị tìm mối contact giữa các yếu tố đã mang lại với những yếu tố chưa biết của tam giác trải qua các hệ thức đã được nêu vào định lí cosin, định lí sin và những công thức tính diện tích s tam giác.
Các việc về giải tam giác:
Có 3 câu hỏi cơ phiên bản về gỉải tam giác:
a) Giải tam giác khi biết một cạnh với hai góc.
Xem thêm: Nơi Bán Máy Cày Nhật Bãi Giá Rẻ, Máy Cày Nhật Bãi
Đối với câu hỏi này ta áp dụng định lí sin nhằm tính cạnh còn lại
b) Giải tam giác khi biết hai cạnh cùng góc xen giữa
Đối với câu hỏi này ta áp dụng định lí cosin để tính cạnh máy ba
c) Giải tam giác lúc biết ba cạnh
Đối với việc này ta sử dụng định lí cosin để tính góc
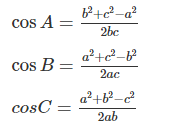
Lưu ý:
Cần để ý là một tam giác giải được khi ta biết 3 yếu tố của nó, trong đó phải có ít nhất một nguyên tố độ dài (tức là yếu tố góc ko được quá 2)Việc giải tam giác được áp dụng vào các bài toán thực tế, tốt nhất là các bài toán đo đạc.Các dạng bài xích tập về hệ thức lượng trong tam giác vuông, cân và thường
Ví dụ 1: ước ao tính khoảng cách từ điểm A đến điểm B nằm sát kia trườn sông, ông Việt vun từ A đường vuông góc cùng với AB. Trên tuyến đường vuông góc này mang một đoạn thằng A C=30 m, rồi vén CD vuông góc cùng với phương BC cắt AB tại D (xem hình vẽ). Đo được AD = 20m, từ đó ông Việt tính được khoảng cách từ A đến B. Em hãy tính độ nhiều năm AB và số đo góc ACB.
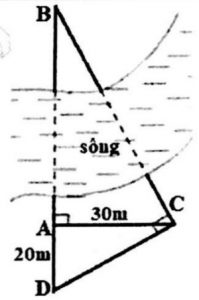
Lời giải:
Xét Δ BCD vuông tại C cùng CA là con đường cao, ta có:
AB.AD = AC2 (hệ thức lượng)

Vậy tính độ nhiều năm AB = 45 m cùng số đo góc ngân hàng á châu là 56018′
Ví dụ 2: mang lại ΔABC tất cả AB = 12, BC = 15, AC = 13
a. Tính số đo các góc của ΔABC
b. Tính độ dài các đường trung tuyến đường của ΔABC
c. Tính diện tích s tam giác ABC, bán kính đường tròn nội tiếp, bán kính đường tròn nước ngoài tiếp tam giác ABC
d. Tính độ dài mặt đường cao nối từ những đỉnh của tam giác ABC
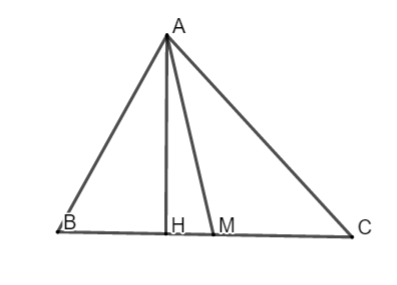
Lời giải:
a. Áp dụng hệ thức lượng vào tam giác ta có:

c. Để tính được diện tích s một cách đúng chuẩn nhất ta sẽ vận dụng công thức Hê – rông



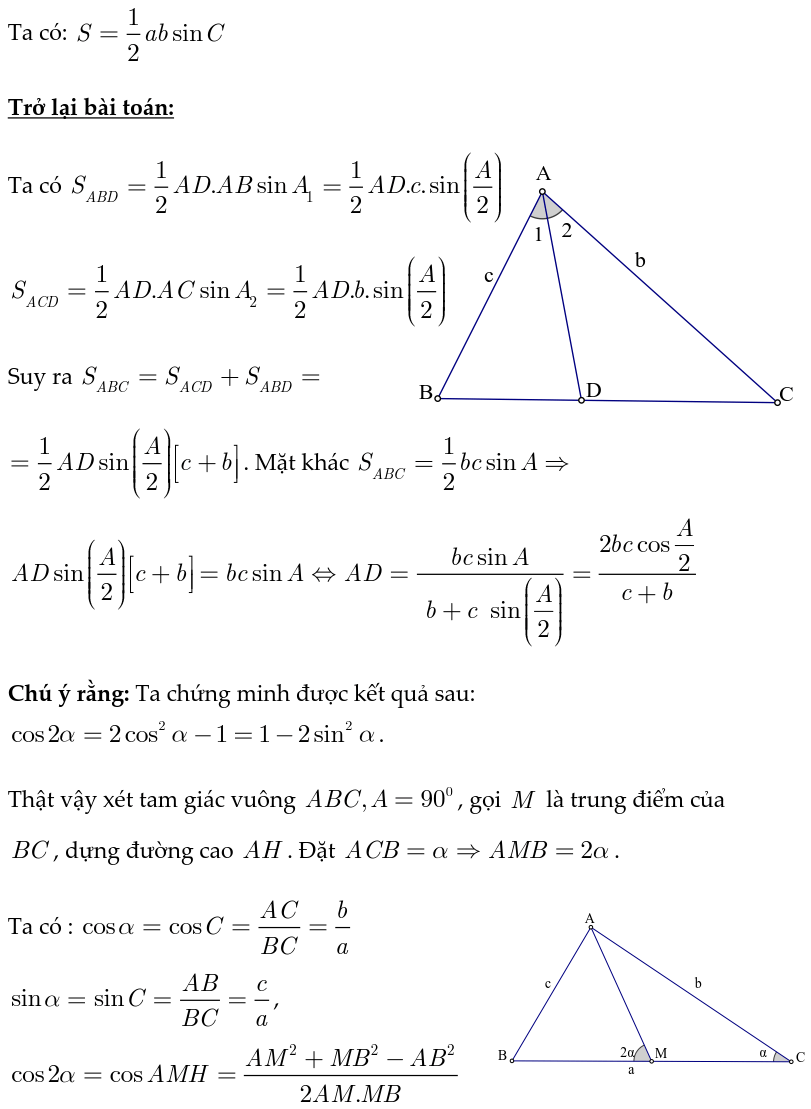
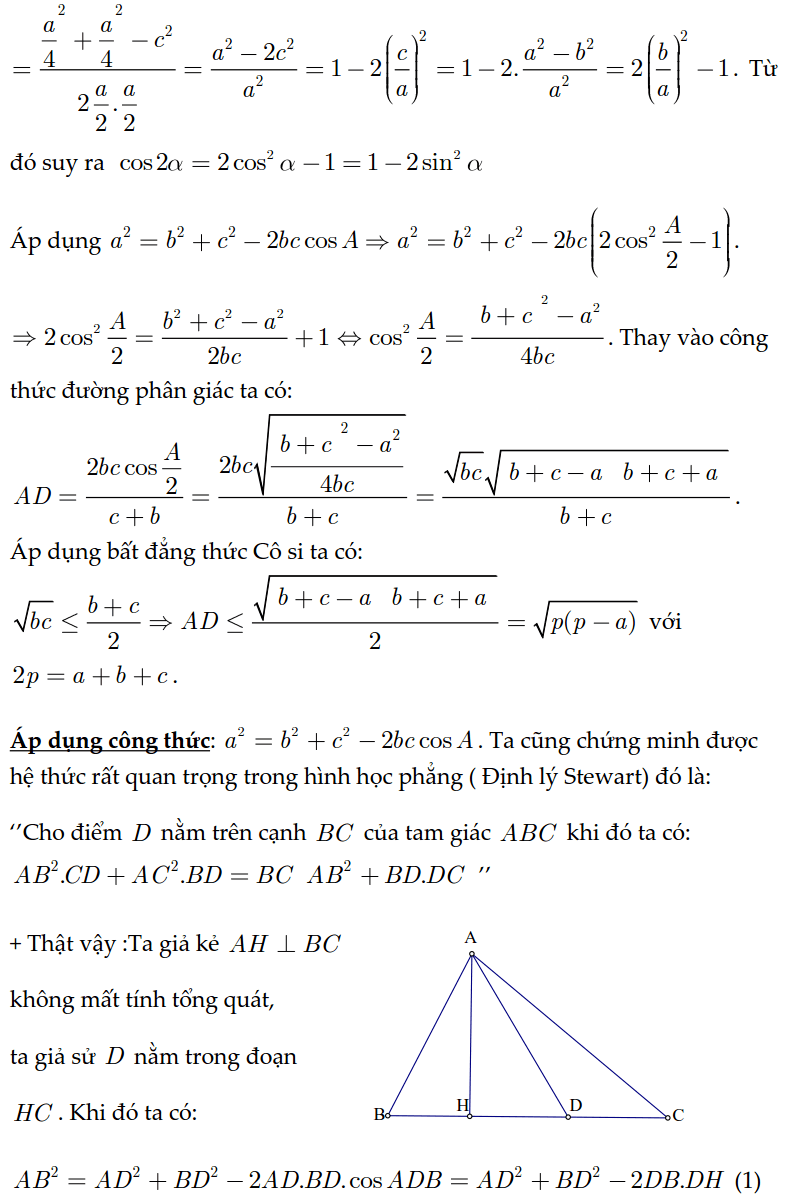

Ví dụ 4: Một người thợ sử dụng thước ngắm gồm góc vuông đề đo độ cao của một cây dừa, với các form size đo được như hình bên. Khoảng cách từ vị trí cội cây đến vị trí chân của fan thợ là 4,8m với từ địa điểm chân đứng thẳng xung quanh đất mang đến mắt của tín đồ ngắm là l,6m. Hỏi với các kích thước trên thì tín đồ thợ đo được chiều cao của cây sẽ là bao nhiêu? (làm tròn mang lại mét).
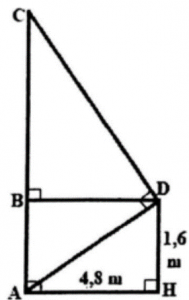
Lời giải:
Xét tứ giác ABDH cóXét tứ giác ABDH có:

Vậy độ cao của cây dừa là 16 m.
Ví dụ 5: đến tam giác ABC vuông trên A, con đường cao AH .
a. Biết AH = 6cm, bh = 4,5cm, Tính AB, AC, BC,HCb. Biết AB = 6cm, bảo hành = 3cm, Tính AH, AC, CH
Lời giải:
a. Áp dụng định lý Pi-Ta-Go đến tam giác vuông AHB vuông tại H
Ta có: AB2 = AH2 + BH2 = 62+ 4,52= 56,25 cm2
Suy ra: AB √56,25 = 7,5( cm)
Áp dụng hệ thức lượng trong tam giác vuông ABC vuông trên A, AH là chiều cao ta được:
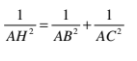

b. Trong tam giác vuông ABH vuông trên H.
Ta có: AB2 = AH2 + BH2
=> AH2 = AB2 – BH2 = 62 – 32 = 27
Vậy AH = √27 = 5,2cm

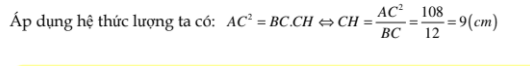
Hy vọng với những kỹ năng về hệ thức lượng trong tam giác mà chúng tôi vừa so với kỹ phía trên rất có thể giúp các bạn nắm kiên cố được công thức để vận dụng giải những bài tập.












